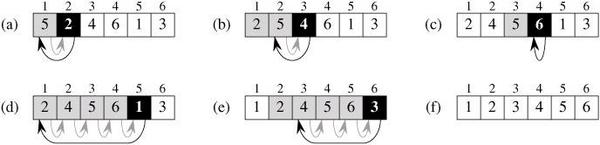
3.1 Asymptotic notation
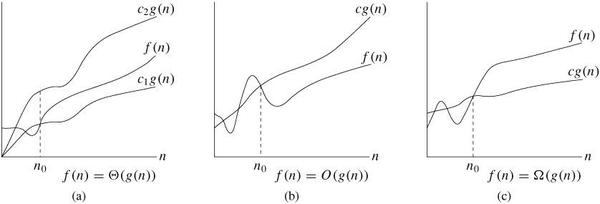
Asymptotic efficiency of algorithms: how the running time of an algorithm increases with the size of the input in the limit.Usually, an algorithm that is asymptotically more efficient will be the best choice for all but very small inputs.Θ(g(n)) = {f(n): there exist positive constants c1, c2, and n0 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0}. /* c1, c2, n0 > 0 */O(g(n)) = {f(n): there exist positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0}. /* upper bound */o(g(n)) = {f(n): for any positive constant c > 0, there exists a constant n0 > 0 such that 0 ≤ f(n) < cg(n) for all n ≥ n0}. /* upper bound */Ω(g(n)) = {f(n): there exist positive constants c and n0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0}. /* lower bound */ω(g(n)) = {f(n): for any positive constant c > 0, there exists a constant n0 > 0 such that 0 ≤ cg(n) < f(n) for all n ≥ n0}. /* lower bound */Θ-notation: For all values of n to the right of n0, the value of f(n) lies above c1g(n) and below c2g(n). For all n ≥ n0, the function f(n) is equal to g(n) to within a constant factor. We say that g(n) is an asymptotically tight bound for f(n).The definition of Θ(g(n)) requires that every member f(n) є Θ(g(n)) be asymptotically positive.We use o-notation to denote an upper bound that is not asymptotically tight.f(n) = Θ(g(n)) implies f(n) = O(g(n)). Θ(g(n)) ⊆ O(g(n)).For any two functions f(n) and g(n), we have f(n) = Θ(g(n)) if and only if f(n) = O(g(n)) and f(n) = Ω(g(n)).Figure 3.1:Θ, O, and Ω notations