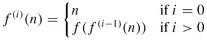3.1 Asymptotic notation
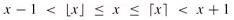
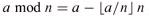
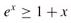
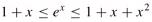
ex = 1 + x + Θ(x2) /* x → 0 */
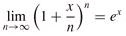
lg kn = (lg n)k /* exponentiation */
lg lg n = lg(lg n) /* composition */
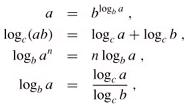
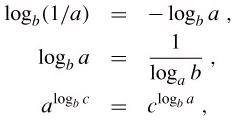
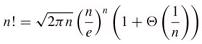
n! = o(nn)
n! = ω(2n)
lg(n!) = Θ(n lg n)
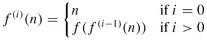
- Asymptotic efficiency of algorithms: how the running time of an algorithm increases with the size of the input in the limit.
- Usually, an algorithm that is asymptotically more efficient will be the best choice for all but very small inputs.
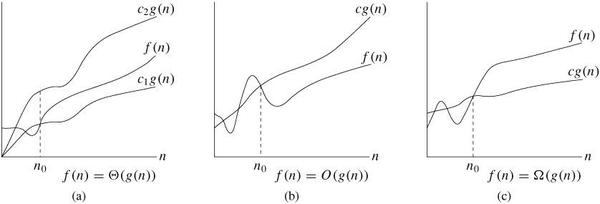
- Θ(g(n)) = {f(n): there exist positive constants c1, c2, and n0 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0}. /* c1, c2, n0 > 0 */
- O(g(n)) = {f(n): there exist positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0}. /* upper bound */
- o(g(n)) = {f(n): for any positive constant c > 0, there exists a constant n0 > 0 such that 0 ≤ f(n) < cg(n) for all n ≥ n0}. /* upper bound */
- Ω(g(n)) = {f(n): there exist positive constants c and n0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0}. /* lower bound */
- ω(g(n)) = {f(n): for any positive constant c > 0, there exists a constant n0 > 0 such that 0 ≤ cg(n) < f(n) for all n ≥ n0}. /* lower bound */
- Θ-notation: For all values of n to the right of n0, the value of f(n) lies above c1g(n) and below c2g(n). For all n ≥ n0, the function f(n) is equal to g(n) to within a constant factor. We say that g(n) is an asymptotically tight bound for f(n).
- The definition of Θ(g(n)) requires that every member f(n) є Θ(g(n)) be asymptotically positive.
- We use o-notation to denote an upper bound that is not asymptotically tight.
- f(n) = Θ(g(n)) implies f(n) = O(g(n)). Θ(g(n)) ⊆ O(g(n)).
- For any two functions f(n) and g(n), we have f(n) = Θ(g(n)) if and only if f(n) = O(g(n)) and f(n) = Ω(g(n)).
- Figure 3.1:Θ, O, and Ω notations

- Symmetry: f(n) = Θ(g(n)) if and only if g(n) = Θ(f(n)).
- Transpose symmetry:
- f(n) = O(g(n)) if and only if g(n) = Ω(f(n))
- f(n) = o(g(n)) if and only if g(n) =ω(f(n))
- Trichotomy: For any two real numbers a and b, exactly one of the following must hold: a < b, a = b, or a > b.
- A function f(n) is monotonically increasing if m ≤ n implies f(m) ≤ f(n). A function f(n) is strictly increasing if m < n implies f(m) < f(n).
- For any real number x, we denote the greatest integer less than or equal to x by ⌊x⌋ (read "the floor of x") and the least integer greater than or equal to x by ⌈x⌉ (read "the ceiling of x"). For all real x:
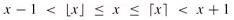
- For any integer a and any positive integer n, the value a mod n is the remainder (or residue) of the quotient a/n:
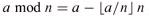
- If (a mod n) = (b mod n), we write a ≡ b (mod n) and say that a is equivalent to b, modulo n. a ≡ b (mod n) if and only if n is a divisor of b - a.
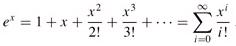
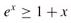
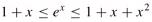
ex = 1 + x + Θ(x2) /* x → 0 */
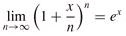
- lg n = log2 n /* binary logarithm */
lg kn = (lg n)k /* exponentiation */
lg lg n = lg(lg n) /* composition */
- For all real a > 0, b > 0, c > 0, and n
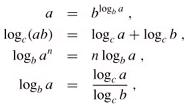
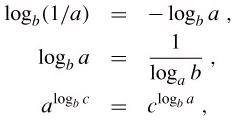
- Use the notation "lg n" when we don't care about constant factors.
- Factorials: A weak upper bound on the factorial function is n! ≤ nn, Stirling's approximation.
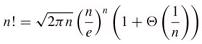
n! = o(nn)
n! = ω(2n)
lg(n!) = Θ(n lg n)
- Functional iteration: We use the notation f(i)(n) to denote the function f(n) iteratively applied i times to an initial value of n.